金融数学第05讲(投资组合理论:考虑无风险资产,VaR风险度量)
3.4风险资产组合与无风险借贷的结合
马科维茨理论中,构成组合的资产都是风险资产。但现实中投资者还可以选择无风险资产,下面我们通过引入无风险资产,说明包括无风险资产的投资组合与不包括无风险资产的投资组合有什么样的区别。
(一)一种无风险资产+一种风险资产的讨论
例 一种风险资产和一种无风险资产
B 女士考虑购买 M 公司的股票,且 B 女士可按照无风险利率借入或贷出,相关参数如下
\begin{array}{lcc} & \text { M公司股票 } & \text { 无风险资产 } \\ \hline \text { 预期收益率 } & 14 \% & 10 \% \\ \text { 标准差 } & 0.20 & 0 \end{array}\\
如果 B 女士投资 1000 元,其中 350 元投资股票,650 元投资无风险资产,那么她的期望收益和标准差是多少?
解 本题可以看做两种风险资产的组合,其中一种风险资产的风险为 0.
预期收益率: E\left(R_{P}\right)=11.4 \%=(0.65 \times 10 \%)+(0.35 \times 14 \%)
标准差: \sigma_{P}=(1-w) \sigma_{M}=(.35) \times(.20)=7 \%
其中无风险资产的标准差和两者协方差均为 0.
下图表明,收益率-标准差图像为一条直线
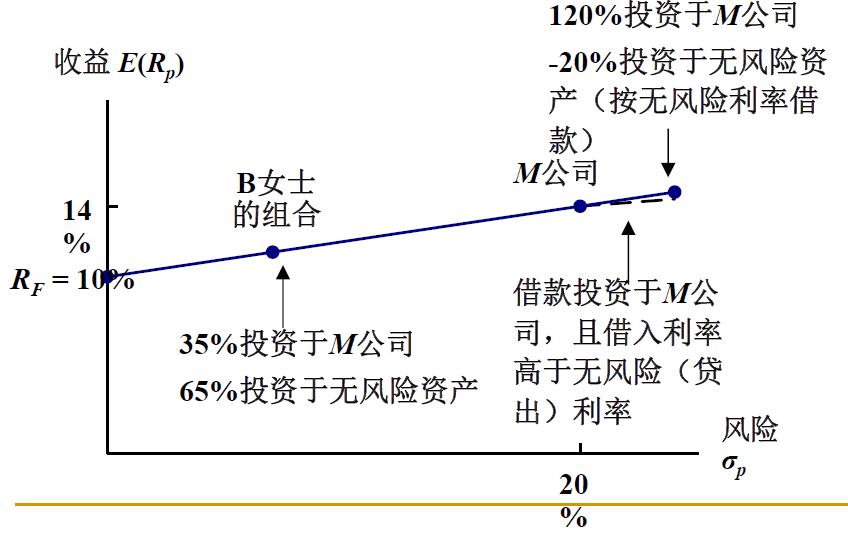
其中股票和无风险资产的延长线上的点表示借钱投资股票。
注意:如果借款利率与存款利率不同,那么需要在 y 轴上找到借款利率R' ,然后连接 R' 和 M股票,得到反向延长线才表示借款买股票。
说明:通过借钱投资,可以获得更高收益,同时也冒更大风险。
问:为什么不能卖股票投资无风险资产?
答:这样做对应的收益率和标准差如下图红线
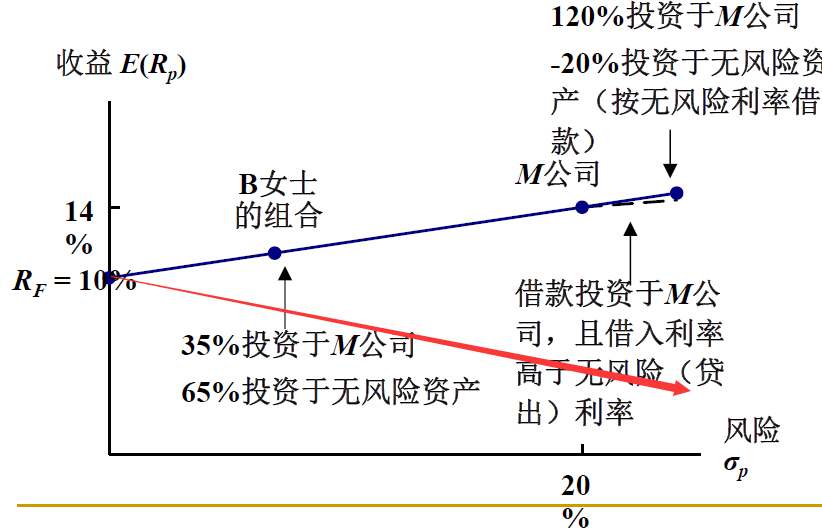
很明显,理性投资者不会选择红线。
(二)一个无风险资产+风险资产组合
可以把风险资产组合看做一个风险资产。
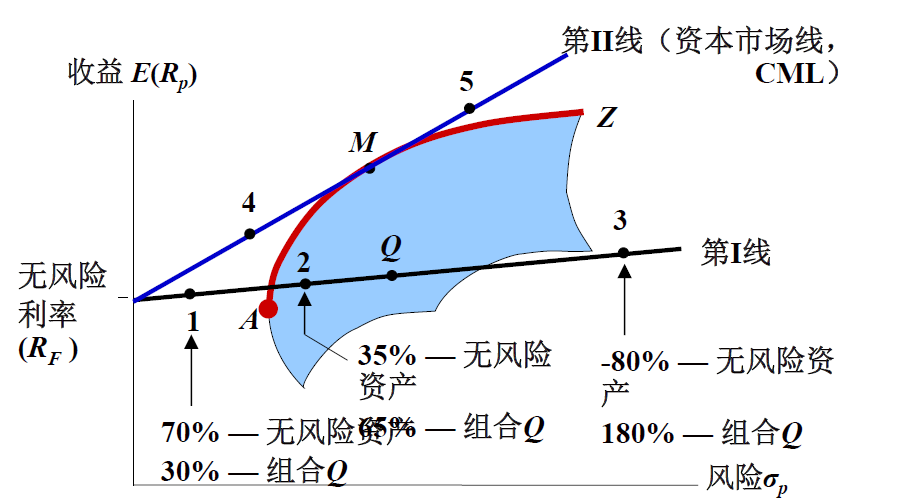
如果只考虑风险资产组合,那么可行集为蓝色区域;而如果加入无风险资产,那么对于任意一个风险资产组合(比如 Q 和 M ),对应的可行集为无风险资产与该风险资产组合连接得到的射线。(图中的蓝线和黑线)
说明:加入了无风险资产后,能够得到不在蓝色区域的资产组合,也就是得到了单纯靠投资风险资产无法达到的投资组合。
我们对于所有蓝色区域的点都能构造一条射线,因此加入了无风险资产后,可行集变成一个角形区域。角形区域的上边界(图中蓝线)自然就是有效前沿边界,我们也把它称为“资本市场线”--所有资产的有效集。
(1)分离定理
投资者的投资决策分为两个步骤:
- 首先只考虑风险资产,找到双曲线边界(图中AMZ),加入无风险资产,找到相切的 M 点,并构造射线,其中 M 点称为最优风险资产组合。
- 根据投资者风险厌恶程度,在射线上取点。
我们看到,无论投资者风险厌恶程度如何,他的投资中,风险资产组合都是一样的(都是 M 点对应的组合)
(2)共同期望假设
这一强大的结论基于一个很强的假设--共同期望假设。即投资者对期望收益率和标准差的估计都是相同的,或投资者有相同的信息来源。
(3)市场组合
而当共同期望假设被满足时,所有投资者的前沿边界都是一样的,其中 M 称为市场组合。而因为实际市场上证券数量很多,证明一个风险资产组合是否为市场组合,是不可能的。在实践中,常用股票指数来代表市场组合。
(4)资本市场线 CML 方程
资本市场线方程的解析表达式为
E\left(R_{P}\right)=R_{F}+\frac{E\left(R_{M}\right)-R_{F}}{\sigma_{M}} \times \sigma_{P}\\
截距是无风险利率,斜率为风险价格(承担单位风险所要求的超额回报率),其中分子为超额收益率,分母为市场组合的风险。
就是无风险资产 P 和市场组合 M 的直线,推导很容易。
(5)加入无风险资产后有效前沿的数学推导
求解最优资产组合系数相当于求解如下规划
\left\{\begin{array}{l} \min \frac{1}{2} \sigma_{p}^{2}=\frac{1}{2} \mathbf{w}^{T} \Sigma \mathbf{w} \\ \text { s.t. } \mathbf{w}^{T} \overline{\mathbf{r}}+\left(1-\mathbf{w}^{T} \overrightarrow{\mathbf{1}}\right) r_{f}=E\left(r_{p}\right) \end{array}\right.\\
其中 \mathbf{w} 为风险资产构成的权重。即给定收益率,使得风险最小。
利用拉格朗日数乘法得到
w_{p}=\frac{E\left(\widehat{r}_{p}\right)-r_{f}}{H} \Sigma^{-1}\left(\overline{\mathbf{r}}-r_{f} \overrightarrow{\mathbf{1}}\right)\\
其中
H=\left(\overline{\mathbf{r}}-r_{f} \overrightarrow{\mathbf{1}}\right)^{T} \Sigma^{-1}\left(\overline{\mathbf{r}}-r_{f} \overrightarrow{\mathbf{1}}\right)=a-2 b r_{f}+c r_{f}^{2} \geq 0\\
- 最优组合中各风险资产比例计算
如果要求最优风险资产组合中,各风险资产的比例,直接求
\Sigma^{-1}\left(\overline{\mathbf{r}}-r_{f} \overrightarrow{\mathbf{1}}\right)\\
然后再归一化即可!
- 有效边界直线计算
如果让求有效边界直线,那么斜率就是 \pm\sqrt{H} ,截距就是 r_f .
- 切点坐标计算
过时的方法:
如果让求切点,那么先把双曲线表达式写出来,联立直线方程得到二次函数,其极值点就是切点横坐标,纵坐标代入直线方程可得。这里我已经算出横坐标的表达式如下:
\[x_M=\frac{{{c^2}\sqrt H \left( {{r_f} - \frac{b}{c}} \right)}}{{cd - {c^2}H}}\\\]
如果算出横坐标是负的,就取绝对值,此时说明切线斜率为 -\sqrt{H} .
最快的方法:
因为切点对应的无风险资产为0,所以直接利用之前归一化的权重 w ,可得
\sigma_p=x_M=\sqrt{w'\Sigma w},\quad E(r_p)= y_M=w'r\\
具体过程:相当于 \[\min \frac{1}{2}{w^T}\Sigma w + \lambda \left[ {{w^T}\bar r + \left( {1 - {w^T}\vec 1} \right){r_f} - E\left( {{r_p}} \right)} \right]\]
对 w 和 \lambda 求偏导,并令为0,得到
\[\left\{ \begin{array}{l} \Sigma w + \lambda \left( {\bar r - {r_f}\vec 1} \right) = 0\\ {w^T}\left( {\bar r - {r_f}\vec 1} \right) = E\left( {{r_p}} \right) - {r_f} \end{array} \right.\\\]
下面式子右边为实数,所以有
\[{\left( {\bar r - {r_f}\vec 1} \right)^T} w= E\left( {{r_p}} \right) - {r_f}\\\]
对上面式子左乘 \[{\Sigma ^{ - 1}}\] 得到
\[w + \lambda {\Sigma ^{ - 1}}\left( {\bar r - {r_f}\vec 1} \right) = 0\\\]
再左乘 {\left( {\bar r - {r_f}\vec 1} \right)^T} 得到
\[{\left( {\bar r - {r_f}\vec 1} \right)^T}w + \lambda {\left( {\bar r - {r_f}\vec 1} \right)^T}{\Sigma ^{ - 1}}\left( {\bar r - {r_f}\vec 1} \right) = 0\\\]
结合 \[{\left( {\bar r - {r_f}\vec 1} \right)^T} w= E\left( {{r_p}} \right) - {r_f}\] 解得
\lambda = -\frac{E\left(\widehat{r}_{p}\right)-r_{f}}{H} \Sigma^{-1}\\
投资组合的收益和风险的关系如下
\[\left\{ \begin{array}{l} \sigma \left( {{r_p}} \right) = \frac{{E\left( {{r_p}} \right) - {r_f}}}{{\sqrt H }},E\left( {{r_p}} \right) - {r_f} \ge 0\\ \sigma \left( {{r_p}} \right) = \frac{{E\left( {{r_p}} \right) - {r_f}}}{{\sqrt H }},E\left( {{r_p}} \right) - {r_f} < 0 \end{array} \right.\\\]
因此前沿边界为通过点 \[\left( {0,{r_f}} \right)\] ,斜率为 \[ \pm \sqrt H \] 的射线。
(6)前沿的几何结构
分三种情况: \begin{array}{ll} r f<b / c, & r_{f}>b / c, \quad r_{f}=b / c \end{array}
其中 b/c 为不包括无风险资产情形下,最小方差组合的期望收益率。
- 当 r f<b / c :只有上方有切线,下方没有
- 当 r f=b / c :两边都只有渐近线而没有切线
- 当 r f>b / c :只有下方有切线,上方没有



注:投资权重 = 投资风险资产的权重,比例为 0 的推导如下
\begin{aligned} \overrightarrow{\mathbf{1}^{T}} \mathbf{w}_{p} &=\frac{E\left(\widetilde{r}_{p}\right)-r_{f}}{H} \mathbf{1}^{T} \Sigma^{-1}\left(\widetilde{\mathbf{r}}-r_{f} \overrightarrow{\mathbf{1}}\right) \\ =& \frac{E\left(\widetilde{r}_{p}\right)-r_{f}}{H}\left(b-\frac{b}{c} c\right)=0 \end{aligned}\\
其中第一种情形比较重要,其余两种都少见。
(7)总结:存在无风险资产的定价问题
设 p 为边界组合(非 mvp ),q 为任意证券组合,两者协方差有如下计算公式
\operatorname{Cov}\left(\widetilde{r}_{p}, \widetilde{r}_{q}\right)=w_{p}^{T} \Sigma w_{q}=\frac{\left[E\left(\widetilde{r}_{p}\right)-r_{f}\right]\left[E\left(\widetilde{r}_{q}\right)-r_{f}\right]}{H}\\
又因 \sigma^{2}\left(\widetilde{r}_{p}\right)=\left[E\left(\widetilde{r}_{p}\right)-r_{f}\right]^{2} / H (开根号后就是两条射线),协方差和方差作商可得
E\left(\tilde{r}_{q}\right)-r_{f}=\frac{\operatorname{cov}\left(\tilde{r}_{p}, \tilde{r}_{q}\right)}{\sigma^{2}\left(\tilde{r}_{p}\right)} \times\left(E\left(\tilde{r}_{p}\right)-r_{f}\right)=\beta_{q p} \times\left(E\left(\tilde{r}_{p}\right)-r_{f}\right)\\
注意:这个关系式同 rf 与 b/c 的大小关系无关。
3.5 C-VaR风险度量下的资产组合理论
3.5.1 VaR的引进
背景:
- 马科维茨理论中,资产收益正向变动也被加入到风险中,这实际上并不合理。
- 金融系统越来越复杂,仅用方差度量风险不够。
- 布雷顿森林体系崩溃,利率波动加剧,对风险控制要求更高。
布雷顿森林体系:二战快结束时创立,确定美元和黄金挂钩,其他各国货币和美元国购,有效控制了风险,促使各国贸易更快恢复。
创立:VaR 技术( Value-at-risk )是 1993 年 J·P·Morgon, G30 集团在考察衍生产品的基础上提出的一种风险测度方法。
吸引力:它把银行的全部资产组合风险概括为一个简单的数字,并以货币计量单位来表示风险管理的核心——潜在亏损。
基本含义:在某一特定的持有期内,在给定的置信水平下,给定的资产或资产组合可能遭受的最大损失值。
比如保险公司想要使得破产概率不超过某个值,就相当于给定某个比较高的置信水平,VAR 的值不会很大。
其数学表达式为 \operatorname{Prob}(\triangle \mathrm{p} \geq \mathrm{VaR})=1-\alpha ,即损失超过 VaR 的概率不超过 1-α.
计算涉及两个因素:
- 目标时段:指我们要计算未来多长时间的 VaR,可以取为 1 天,1 周,10 天,1 月等
- 置信水平:取决于风险管理者的风险态度,一般在 90%-99%
例如 J.P .M organ 公司 1994 年年报披露,该公司一天的 95%VaR 值为 1500 万美元。即该公司可以以 95% 的可能性保证,1994 年每一特定时点上的证券组合在未来 24 小时之内,由于市场价格变动而带来的损失不会超过 1500 万美元。
两个假设:
- 市场有效性假设
- 市场波动是随机的,不存在自相关
3.5.2 数学基础
以下两个概念在数理统计或概率论中涉及,自查。
- 随机变量的分位数
- 条件概率和条件期望
(一)随机损失的 VaR 与 C-VaR
假设市场上有 n 个资产,收益率向量为 \widetilde{\mathbf{r}}=\left(\widetilde{r}_{1}, \tilde{r}_{2}, \ldots, \quad \tilde{r}_{n}\right)^{T} ,并假设 L=L(\boldsymbol{w}, \boldsymbol{r}) 为资产组合的损失函数。
例如一个可能的损失函数为 L(\boldsymbol{w}, \boldsymbol{r})=1-\boldsymbol{w}^{T}(1+\boldsymbol{r})=-\boldsymbol{w}^{T} \boldsymbol{r}
其中 1 为成本,减去的那一项为收益。
记收益率向量的联合密度为 p(\boldsymbol{r}) ,损失的分布函数为 \Psi(\lambda)=P\{L(\boldsymbol{w}, \boldsymbol{r}) \leq \lambda\} ,此时满足
\Psi(\lambda)=\int_{\{L(w, \mathbf{r}) \leq \lambda\}} p(\mathbf{r}) d \mathbf{r}\\
给定置信水平 α ,VaR 定义为随机损失的 α 分位数,即
V a R_{\alpha}=\inf \{\lambda \in R \mid \Psi(\lambda) \geq \alpha\}\\

(二)VaR 的计算
(1)解析法
注意:如果上、下分位数分不清就画图,保证密度函数从 -∞ 积分到 VaR 的面积是一个比较小的数即可(可能是 α 也可能是 1-α,数理统计中严格定义置信水平为 1-α,但这里有时候定义为 α,有时候定义为 1-α,很乱...)
例 单个正态分布收益资产的 VaR
首先考虑只有一个风险资产情形,那么 w=1,并假设收益率 r 服从正态分布,即 \tilde{r} \sim N\left(\mu, \sigma^{2}\right) ,仍然设损失为 L=-w \tilde{r}=-\tilde{r} ,从而 VaR 满足
P\left\{L \leq V a R_{\alpha}\right\}=\alpha\\
即
P\left\{L \leq V a R_{\alpha}\right\}=P\left\{-\tilde{r} \leq V a R_{\alpha}\right\}=P\left\{\frac{-\tilde{r}+\mu}{\sigma} \leq \frac{V a R_{\alpha}+\mu}{\sigma}\right\}=\alpha\\
可以得到 \frac{V a R_{\alpha}+\mu}{\sigma}=Z_{\alpha} ,注意这里是下分位数!(数理统计后遗症预警),进而
V a R_{\alpha}=-\mu+\sigma Z_{\alpha}\\
例 多个联合正态分布收益率的 VaR 计算
考虑有 n 个风险资产,收益率向量 \tilde{\mathbf{r}}=\left(\widetilde{r}_{1}, \tilde{r}_{2}, \ldots, \quad \tilde{r}_{n}\right)^{T} 服从正态分布,即
\widetilde{\mathbf{r}} \sim N(\overline{\mathbf{r}}, \Sigma)\\
组合收益为 \widetilde{r}_{p}=\mathbf{w}^{T} \mathbf{r} ,定义损失函数为 L(w, r)=1-w^{T}(1+r)=-w^{T} r
由于正态分布的线性组合仍服从正态,所以
\widetilde{r}_{p} \sim N\left(w^{T} \bar{r}, w^{T} \sum w\right)\\
利用前面例子的结论可得
V a R_{\alpha}=-\mathbf{w}^{T} \overline{\mathbf{r}}+\sqrt{\mathbf{w}^{T} \Sigma \mathbf{w}} Z_{\alpha}\\
例 多个联合正态分布收益率基础上,又含有无风险资产
只要把组合收益率表示出来就差不多了
\hat{r}_{p} \sim N\left(w_{0} r_{f}+\mathbf{w}^{T} \overline{\mathbf{r}}, \mathbf{w}^{T} \sum \mathbf{w}\right)\\
类似地
V a R_{\alpha}=-w_{0} r_{f}-\mathbf{w}^{T} \overline{\mathbf{r}}+\sqrt{\mathbf{w}^{T} \Sigma \mathbf{w}} Z_{\alpha}\\
(2)历史模拟法
已经发生过的事件中,我们可以提取多个损失构成样本,通过样本分位数来近似总体分位数,也就是 VaR
缺陷:未来不一定是历史的再现
(3)蒙特卡洛模拟
从损失函数中用随机模拟来采样,模拟分位数。
(三)VaR风险度量的优缺点
优点:
- 简单直观
- 可以测量非线性风险
缺点:
- 不是一致性风险度量
(四)一致性风险度量
对任意随机损失 X ,风险度量 ρ(X) 满足下面四个性质:
- 平移不变:ρ(X+c) = ρ(X)+c--损失增加常数,风险增加常数
- 次可加性:ρ(X+Y) ≤ ρ(X)+ρ(Y)--风险要能对冲
- 正齐次性:cρ(X) = ρ(cX)--损失扩大,风险扩大,但是否线性有异议
- 单调性:对 X<Y, ρ(X)<ρ(Y)--损失越大,风险越大
称 ρ(X) 为一致性风险度量。
文章被以下专栏收录


